Code:
' Original main Code Courtesy of Dev Ashish http://access.mvps.org/access/api/api0013.htm
' (and Hans, https://eileenslounge.com/viewtopic.php?p=321978#p321978)
Private Declare Function apiGetClassName Lib "user32" Alias "GetClassNameA" (ByVal hwnd As Long, ByVal lpClassName As String, ByVal nMaxCount As Long) As Long ' lpClassName - Points to the buffer that is to receive the class name string.
Private Declare Function apiGetDesktopWindow Lib "user32" Alias "GetDesktopWindow" () As Long ' The desktop window is the area on top of which all icons and other windows are painted.
Private Declare Function apiGetWindow Lib "user32" Alias "GetWindow" (ByVal hwnd As Long, ByVal wCmd As Long) As Long ' retrieves the handle of a window that has the specified relationship (Z order or owner) to the specified window. ' uCmd Specifies the relationship GW_CHILD The retrieved handle identifies the child window at the top of the Z order, if the specified window is a parent window; otherwise, the retrieved handle is NULL. The function examines only child windows of the specified window. It does not examine descendant windows.
Private Declare Function apiGetWindowLong Lib "user32" Alias "GetWindowLongA" (ByVal hwnd As Long, ByVal nIndex As Long) As Long ' information about the specified window. - retrieves the 32-bit (long) value at the specified offset into the extra window memory of a window. nIndex - Valid values are in the range zero through the number of bytes of extra window memory, minus four
Private Declare Function apiGetWindowText Lib "user32" Alias "GetWindowTextA" (ByVal hwnd As Long, ByVal lpString As String, ByVal aint As Long) As Long ' copies the text of the specified window’s title bar (if it has one) into a buffer. If the specified window is a control, the text of the control is copied.
Private Declare Function FindWndNumber Lib "user32" Alias "FindWindowA" (Optional ByVal lpClassName As String, Optional ByVal lpWindowName As String) As Long ' retrieves the handle to the top-level window whose class name and window name match the specified strings. This function does not search child windows. lpWindowName- the window name (the window’s title), if parameter is NULL, all window names match. http://allapi.mentalis.org/apilist/FindWindow.shtml
Private Declare Function IsWindowVisible Lib "user32.dll" (ByVal hwnd As Long) As Long
Private Const mcGWCHILD = 5
Private Const mcGWHWNDNEXT = 2 ' GW_HWNDNEXT - The retrieved handle identifies the window below the specified window in the Z order. If the specified window is a topmost window, the handle identifies the topmost window below the specified window. If the specified window is a top-level window, the handle identifies the top-level window below the specified window. If the specified window is a child window, the handle identifies the sibling window below the specified window.
Private Const mcGWLSTYLE = (-16)
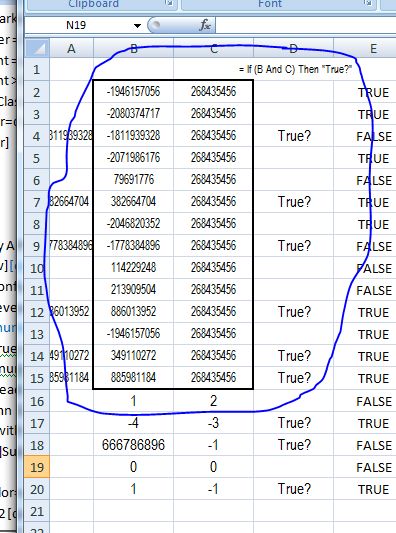
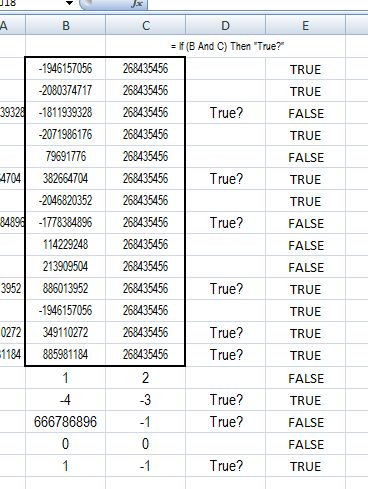
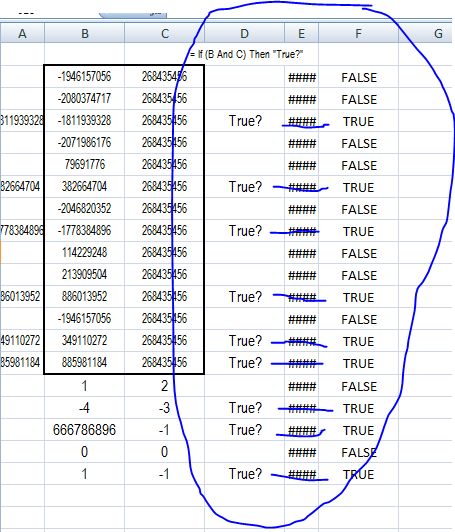
Private Const mcWSVISIBLE = &H10000000 ' Watch window gives 268435456 (even when no code is running)
Private Const mconMAXLEN = 255
Public Sub fEnumWindowsPost15Post() ' https://eileenslounge.com/viewtopic.php?p=322275#p322275
Rem 1 ' Some headings for worksheet output, and for me to remeber when/ what computer I was on, not important for understanding the main coding
Dim Ws As Worksheet: Set Ws = ThisWorkbook.Worksheets.Item(1)
Dim Lc As Long, Lr As Long: Let Lc = Ws.Cells.Item(2, Ws.Columns.Count).End(xlToLeft).Column
Let Ws.Cells.Item(1, Lc + 1) = CreateObject("WScript.Network").ComputerName & " " & Format(Now(), "ddd,dd,mmm,yyyy") ' Environ$("computername") Nigel Heffernan https://stackoverflow.com/questions/3551055/how-to-get-name-of-the-computer-in-vba/10108951#10108951
Let Ws.Cells.Item(2, Lc + 1) = "Hwnd": Let Ws.Cells.Item(2, Lc + 2) = "Class Name": Let Ws.Cells.Item(2, Lc + 3) = "Caption": Let Ws.Cells.Item(2, Lc + 4) = "Hwnd(from Caption)" ' : Let Ws.Cells.Item(2, Lc + 5) = "enum visible?"
Rem 2 ' The next was originally from Dev Ashish http://access.mvps.org/access/api/api0013.htm
Dim lngx As Long, lngLen As Long, lngStyle As Long, strCaption As String
'2a) This somehow gets me to my start point, whatever I am allowed to call it
Let lngx = apiGetDesktopWindow(): Debug.Print "Geted Desktop Window " & lngx & " " & " CLass name " & fGetClassName(lngx)
'2b) Loop to get info from windows at some sort of "top, main, visible or some such"
'2b)(i)
Let lngx = apiGetWindow(lngx, mcGWCHILD): Debug.Print " First child to Desktop " & lngx & " CLass name " & fGetClassName(lngx) ' GW_CHILD = 5 The topmost of the given window's child windows. This has the same effect as using the GetTopWindow function, ... usually at the top of all the other children in the Z-order
'2b)(ii)
Do While Not lngx = 0 ' We are looping "equal level children", seperated not realy, just look seperate to us because of the seen to us z order
Let strCaption = fGetCaption(lngx)
If Len(strCaption) > 0 Then ' Those without a caption seem not important
Let lngStyle = apiGetWindowLong(lngx, mcGWLSTYLE) ' apiGetWindowLong gets info, GWL_STYLE -16 retrieves the window styles
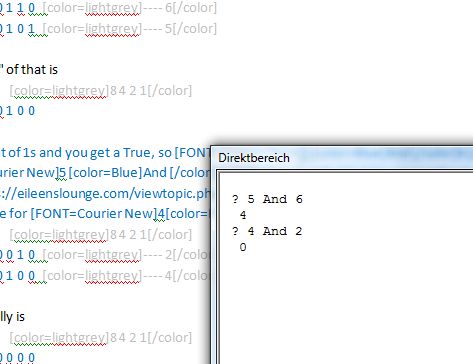
If lngStyle And mcWSVISIBLE Then ' ' For enum visible windows only - see here for full discusions of what this is about https://eileenslounge.com/viewtopic.php?p=322270#p322270
' If IsWindowVisible(lngx) Then ' alternative https://www.eileenslounge.com/viewtopic.php?p=322379#p322379
Let Lr = Ws.Cells.Item(Ws.Rows.Count, Lc + 1).End(xlUp).Row
Debug.Print FindWndNumber(lpClassName:=fGetClassName(lngx), lpWindowName:=vbNullString), fGetClassName(lngx); Tab(50); fGetCaption(lngx); Tab(100); FindWndNumber(lpClassName:=vbNullString, lpWindowName:=fGetCaption(lngx))
Dim strHandle As String: Let strHandle = FindWndNumber(lpClassName:=fGetClassName(lngx), lpWindowName:=vbNullString) ' This is not really necerssary, other thsn perhaps useful for later debuggung
'Let Ws.Cells.Item(Lr + 1, Lc + 1) = strHandle & " " & Application.Evaluate("=DEC2HEX(" & strHandle & ")") & " " & NumberInBinary2sCompliment(strHandle)
Let Ws.Cells.Item(Lr + 1, Lc + 1) = strHandle & " " & Hex(strHandle) & " " & NumberInBinary2sCompliment(strHandle)
Let Ws.Cells.Item(Lr + 1, Lc + 2) = fGetClassName(lngx)
Let Ws.Cells.Item(Lr + 1, Lc + 3) = fGetCaption(lngx)
Let Ws.Cells.Item(Lr + 1, Lc + 4) = FindWndNumber(lpClassName:=vbNullString, lpWindowName:=fGetCaption(lngx))
End If
End If
Let lngx = apiGetWindow(lngx, mcGWHWNDNEXT) ' GW_HWNDNEXT = 2 The window below the given window in the Z-order...... in oother words, the handle returned identifies the sibling window below the specified window.
Loop ' While Not lngx = 0 ' I am going through all the child windows of the desktop windows
End Sub
Private Function fGetCaption(hwnd As Long) As String
Dim strBuffer As String, intCount As Integer
Let strBuffer = String$(Number:=255 - 1, Character:="0") ' "00000000000000000000000000000000..........000"
Let intCount = apiGetWindowText(hwnd:=hwnd, lpString:=strBuffer, aint:=255) ' This makes strBuffer something like *MSCTFIME UI 0000000000000000............000"
If intCount > 0 Then Let fGetCaption = Left$(strBuffer, intCount)
End Function
Private Function fGetClassName(hwnd As Long) As String
Dim strBuffer As String, intCount As Integer
Let strBuffer = String$(255 - 1, 0)
Let intCount = apiGetClassName(hwnd, strBuffer, mconMAXLEN)
If intCount > 0 Then
Let fGetClassName = Left$(strBuffer, intCount)
End If
End Function





 Reply With Quote
Reply With Quote


Bookmarks